Selon la plupart des spécialistes, la thèse d’I. Sutherland, chercheur au MIT, parue en 1962 constitue le point de départ de l’infographie. « SketchPad » était un programme qui permettait d’afficher une croix qui suivait les mouvements d’un crayon optique. Chaque position du curseur a pu être enregistrée grâce à un boîtier équipé de touches. Cette opération qui peut paraître dérisoire aujourd’hui peut être considérée comme le tournant décisif dans le domaine de l’informatique graphique. La course aux images numériques est alors lancée. De nombreux travaux universitaires mènent au développement d’algorithmes multiples de rendu, notamment le célèbre «Ray-tracing». Mais la recherche dans ce domaine est loin d’être terminée.
Par rapport à «l’image traditionnelle », l’image de synthèse offre l’avantage de ne créer qu’une seule fois chaque élément d’une image. Ceux-ci peuvent être stockés sous forme numérique et réutilisés dans n’importe quelle situation.
Ce principe de réutilisation et la création d’images numériques en trois dimensions offrent de nouvelles possibilités : pouvoir travailler comme au cinéma, les contraintes physiques en moins [L&M94].
Une fois l’image numérique définie, en général au moyen d’objets prédéfinis, nous pouvons nous y déplacer à notre guise : aucun point de vue n’est interdit a priori. Nous pouvons à tout moment retravailler chaque élément d’une scène, l’affiner jusqu’à obtenir le résultat souhaité, et vérifier en cours de travail l’aspect final d’une image particulière. La palette d’effets spéciaux disponibles pour retoucher les images – incrustations, superpositions, compositions diverses – est évidemment très large.
Enfin, chaque image, dans son aspect final, peut être calculée et exploitée dans le format que nous souhaitons, et dans un degré de finition allant du plus simple au plus complexe.
Ce chapitre va tout d’abord expliquer l’historique et les principes de base du film 3D. Ensuite, nous trouverons les techniques de modélisations, le rendu et les mécanismes de l’animation. Enfin nous trouverons quelques applications actuelles et futures de la réalité virtuelle.
En 1979, les travaux de Charles Csuri à l’Université de l’état de l’Ohio ont lancé l’idée de l’animation en trois dimensions. Le premier film 3D « Vol de rêve » réalisé par Nadia et Daniel Thalmann en 1982, permet de passer de la théorie à la pratique. Toujours en 1982, le film « Tron » ( Walt Disney Production) fut le premier grand film à utiliser des images de synthèse : notamment dans une course de motos futuristes. Mais jusque-là les images de synthèse n’utilisaient pas encore des algorithmes de textures ou de « Ray-Tracing ».
Depuis le début des images de synthèse, des sociétés telles que ILM, Division ou Neurone Production, spécialisées dans les images de synthèse voient le jour. Citons par exemple ILM créée pour les effets spéciaux de la série « Star Wars », « Abyss », « Terminator 2 » et « Jurassic Park ».
Hors des colossaux budgets cinématographiques, les animations 3D se retrouvent dans des domaines tels que la publicité, les génériques d’émissions, les bandes vidéos, les simulateurs, les jeux,...
Mais les images de synthèse se retrouvent également dans des domaines moins liés à l’image comme par exemple la recherche, la médecine, les parcs d’attractions, la météo ou l’archéologie.
Dans tous ces domaines, les principes de création d’un film 3d restent les mêmes.
Imaginez l’espace comme un décor ou un plateau de cinéma et placez-y ses objets de décors et ses personnages, placez des lumières. Pour chaque objet, définissez ses attributs : sa couleur, sa texture, sa luminosité,... Placez une caméra imaginaire permettant de voir la scène. Vous obtenez alors une image. Déterminez les changements image par image des objets non statiques : recopiez l’image de départ en appliquant à chaque image ces changements. Vous obtenez les images du film 3D.
Enfin affichez les images les unes à la suite des autres. Vous obtenez alors votre premier film d’images de synthèse.
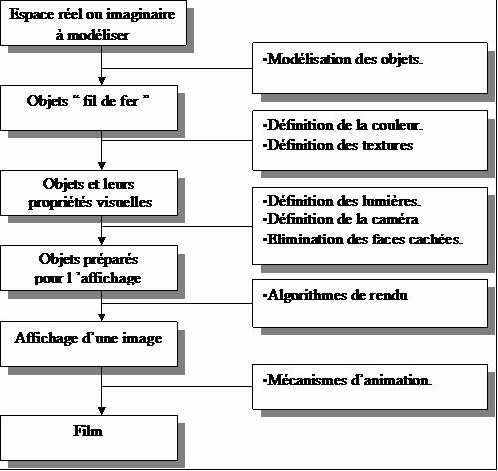
Voici graphiquement les étapes et les articulations de cette présentation :


« La première difficulté réside dans la projection de l’idée sur un support adéquat qui doit en fin de compte aboutir à un projet compréhensible pour la réalisation de l’objet » [Cou95].
Traditionnellement, cette projection se fait via un support, une feuille de papier et un outil, un crayon. Dans le contexte de l’informatique, le support et les outils sont différents. Il s’agit de créer une représentation géométrique 2D ou 3D de l’objet dans la mémoire de l’ordinateur, c’est-à-dire lui donner forme en 3 dimensions, le définir comme un volume ou un assemblage de volumes sous forme compréhensible du point de vue informatique.
Le passage de cet objet externe (hors ordinateur) à sa représentation interne (dans l’ordinateur), s’appelle la modélisation.
La technique de base en modélisation consiste à utiliser des primitives géométriques ou volumes simples :
- soit sous forme polygonale : chaque volume apparaît alors comme un ensemble non structuré de facettes contiguës.
- soit sous forme de surfaces paramétriques (patches, B-splines,...) : le volume est alors structuré comme un quadrillage de surfaces, chaque carreau étant bordé de courbes définies par une équation particulière (courbes de Bézier par ex.)
La suite de cette partie va, tout d’abord , expliquer l’espace tridimensionnel et son système de repère.
Une fois l’espace défini, nous parlerons des principales techniques de modélisations d’objets.
Enfin nous pourrons aborder les propriétés visuelles que l’on peut associer aux objets modélisés : les matériaux et les textures.
Par la simulation de l’espace tridimensionnel , la modélisation aboutit à la création d’une véritable maquette virtuelle. Le repérage des objets composant cette maquette dans l’espace se fait habituellement à l’aide de coordonnées dans un repère d’axes XYZ.
Deux systèmes d’axes XYZ coexistent :
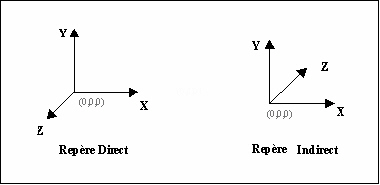
Le repère « direct » :
Le repère est dit « direct » s’il respecte la règle des trois doigts, c’est-à-dire si l’on peut avec le pouce, le majeur et l’index de la main gauche pointer les trois directions Z, X et Y.
C’est le repère utilisé en général dans le monde réel.
Le repère « indirect » :
Dans ce cas, l’axe des Z a une orientation opposée à celle du repère direct. C’est le système d’axes généralement utilisé en infographie : les axes X et Y correspondent aux axes du « viewport » utilisé pour la représentation. L’axe des Z quant à lui peut être interprété comme la distance de l’objet numérique par rapport au « viewport » ou à l’œil de l’observateur.
Le repère direct est généralement utilisé dans le « monde réel », il convient donc, pour toutes les modélisations d’objets numériques, d’effectuer un changement de système de coordonnées afin d’exprimer l’objet dans les mêmes coordonnées que le « monde virtuel » : en effet, la représentation de l’espace en imagerie informatique se fait dans le système de coordonnées indirect.
Dans la modélisation en trois dimensions, il est fréquent de positionner un objet par rapport à un point de l’espace ou par rapport à un autre objet. Ce positionnement relatif donne naissance à deux autres types de repères : le repère global et le repère local.
Le repère global :
Il s’agit d’un repère fixe dans lequel les points sont définis par des coordonnées (X, Y, Z) uniques. Ce repère général est également appelé dans la littérature « Système de Coordonnées Général ».
Le repère local :
Chaque objet ou ensemble d’objets, lors de sa modélisation, peut être défini pour des raisons de facilité et de réutilisation dans un repère local qui lui est propre. Ce repère particulier est encore appelé dans la littérature « Système de Coordonnées Utilisateur » (SCU).
L’utilisation de repères locaux permet également de définir pour l’objet modélisé un point de référence. Ce point de référence interne à l’objet est généralement utilisé pour effectuer des rotations autour de lui-même ou des dilatations.
Une fois l’espace défini, nous pouvons maintenant aborder la modélisation des objets proprement dite.
La plupart des logiciels de modélisation utilisent la méthode surfacique ou volumique. Ces deux méthodes sont assez différentes, la méthode surfacique mémorise les faces et la méthode volumique les objets de base qui composent l’objet.
La méthode surfacique ou « B-rep » mémorise uniquement des surfaces dans l'espace. Ce sont les surfaces qui entourent l'objet. «B-rep» signifie Boundary-representation ou description par les frontières. Cette méthode est de loin la plus utilisée en image de synthèse, car elle est en général moins coûteuse en temps de calcul et en espace mémoire que les autres méthodes.
Pour le stockage des surfaces, plusieurs techniques sont possibles : l’énumération de surfaces ou les surfaces paramétriques.
L’énumération de surfaces :
Cette méthode consistent à définir facette par facette la surface de l’objet : ces facettes sont définies à l’aide des sommets et des arêtes qui la composent (de trois à l’infini).
Cette méthode est la plus simple à mettre en œuvre car elle décompose un objet en plus petites surfaces planes. Cette décomposition de surfaces permet aux algorithmes de vu et caché d’éviter des calculs compliqués pour définir si un point est vu ou non. Cette décomposition permet également d’éviter le calcul des tangentes aux surfaces lors du calcul de la couleur de la surface dans les algorithmes de rendu.
Ces surfaces demandent le minimum de calculs, c’est la raison pour laquelle ces surfaces sont généralement utilisées pour les applications temps réel.
Les surfaces paramétriques :
Les surfaces paramétriques quant à elle sont stockées sous forme d’équations. Cette méthode comporte des avantages et des inconvénients : les équations paramétriques des surfaces permettent d’avoir une plus grande précision dans la représentation des formes. Cette précision se traduit par un meilleur rendu des formes même si la surface est proche de l’œil de l’observateur. En contrepartie leur temps de calcul est plus long : pour chaque pixel de l’écran, le calcul de l’équation de la surface doit être effectué. Pour ces raisons, elles ne sont que très rarement utilisées dans les applications en temps réel.
Nous allons maintenant faire un tour d’horizon des techniques les plus fréquemment utilisées pour définir les faces des objets.( [Cou95], [HIL90], [MVC96])
Les surfaces de Coons :
Il s’agit de la première méthode de modélisations des surfaces gauches dans l’espace tridimensionnel : elles sont dues à Coons dans le cadre de ses activités chez Ford (1967).
Le principe de ces surfaces est d’interpoler les quatre courbes qui délimitent la surface en question. Par rapport aux autres surfaces, elles ne sont pas définies par un réseau de points de contrôle. Elles sont particulièrement utiles pour « remplir » des réseaux de courbes sous la forme de surfaces.
Ces surfaces possèdent un inconvénient majeur, elles ne permettent pas de définir en une seule surface les surfaces telles qu’une bosse : l’interpolation des courbes extrêmes empêche, par exemple, qu’un point interne à la surface soit plus haut que les courbes qui l’entourent : la hauteur du point est compris entres la hauteur maximum et minimum des courbes formant le contour.
Les surfaces de Bézier et B-Spline :
Ce type de surfaces est due à l’ingénieur Pierre Bézier de la régie Renaud (1972).
C’est une généralisation des courbes de Bézier en trois dimensions : il s’agit d’une surface générée à partir d’une grille de NxM points de contrôle.
Toutes les modifications effectuées sur un de ces points de contrôle se répercutent sur les points proches de celui-ci et par la suite sur le reste de la surface. Il n‘est donc pas possible de contrôler localement une telle surface.
Les B-Splines sont une généralisation des courbes de Bézier permettant un contrôle local de la surface.
Par contre, ces surfaces permettent de modifier le centre d’une surface ce que ne permettent pas les surfaces de Coons.
Les surfaces Bêta-Splines :
Il s’agit d’une extension des courbes de Bézier qui permet un contrôle local de la surface.
Les Bêta-Splines permettent une gestion de chacun des points de contrôle sans interférences sur ses voisins. Elles introduisent également les concepts de tension (contrôle de la courbure) et de biais (contrôle de la pente). Ces deux concepts permettent d’ajuster la surface en plus du déplacement des points de contrôle.
L’avantage majeur de ces surfaces est que les paramètres qui modifient la forme de la surface peuvent changer sans engendrer un temps de calcul supérieur.
Les NURBS :
Les NURBS ou Non-Uniform Rationnal B-Splines permettent la réalisation des surfaces les plus diverses en permettant un contrôle en tout point de la surface. Les NURBS sont la forme la plus évoluée des B-Splines. Elles se caractérisent par les propriétés suivantes .
Non-uniformité : cette propriété permet de subdiviser une partie de la surface, d’en accroître localement le nombre de points de contrôle, de la couper en certains endroits afin de produire deux parties et de créer des angles vifs si désirés.
Forme rationnelle : cette propriété permet de décrire avec exactitude des primitives quadratiques (cercles, ellipses, sphères,...). Les splines rationnelles permettent de modéliser un nombre plus grand de formes.
Le « poids » : la forme de la surface peut être influencée par un paramètre complémentaire qui est présent en chacun de ses points de contrôles. Ce paramètre permet par exemple de modéliser différents matériaux avec leurs propriété internes : du papier ou de la soie ne se comportent pas de la même façon.
Ces surfaces sont les surfaces actuellement les plus complètes, elle permettent des modifications précises sur les surfaces. Ces surfaces sont implémentées dans des librairies graphiques telles qu’OpenGL™ .
La méthode volumique ne se base plus sur les surfaces ou facettes de surfaces mais sur les volumes, la composition en volumes de base : elle se base sur l'addition ou la suppression de volumes élémentaires simples : prendre un cylindre, ajouter un cube, soustraire une sphère, ...
Cette méthode permet de représenter des volumes très complexes :

La figure ci-dessus montre comment on peut assembler un volume par addition ou par soustraction de volumes plus simples. Les opérations booléennes (union, intersection, différence, …) classiques sont applicables.
Cette méthode de construction, “Arbre de construction” ou encore “CSG” (Constructive Solid Geometry), décrit les objets sous forme d’arbres où les nœuds représentent les opérations booléennes. L’objet ainsi modélisé n’est pas explicitement décrit par son enveloppe mais par la succession des opérations ou transformations qui l’ont généré. Ce type de modélisation a l’avantage de prendre peu de place et de conserver l’historique des opérations effectuées, ce qui est très utile pour les modifications. Par contre, cette technique est mal adaptée à la modélisation d’objets complexes tels que visage, corps humain, …
Il existe d’autres techniques fort proches de « CSG » qui ne considèrent que des formes construites à base de cubes : la décomposition spatiale, l’énumération spatiale et l’«Octree » .
La décomposition spatiale consiste en un découpage de l’espace tridimensionnel en cellules élémentaires. L’objet est alors modélisé en marquant les cellules qui le composent. Chaque cellule peut alors être décomposée pour offrir une précision supérieure. Cette technique permet de composer des formes compliquées mais ne permet pas d’avoir une précision extrême dans la définition de ses contours.
L’énumération spatiale est une variante de la décomposition spatiale, ici l’espace est décomposé en cubes (et non plus en cellules sans formes particulières) ces cubes sont disposés sur une grille fixe. Plus la dimension des cubes est petite, plus l’objet sera précis.
L’«Octree» est une généralisation de l’énumération spatiale qui a la particularité que les cubes peuvent avoir des tailles différentes. Le principe de construction est le suivant : on englobe l’objet à modéliser dans un premier cube. Si l’objet ne remplit pas complètement celui-ci, on subdivise le cube en octants. Si chacun de ces octants résultants est complètement vide ou plein, on arrête le subdivision. Par contre s’il reste des octant partiellement pleins on continue le processus pour ceux-ci.
Voici un exemple en deux dimensions de cette technique :


Jusqu’à présent nous n’avons considéré que des objets uniquement définis par les coordonnées de leurs faces. Nous pouvons alors donner une apparence à ces coordonnées.
A chaque objet ou sous-ensemble d'un objet, vous associez normalement un matériau. Le matériau détermine non seulement la couleur de l'objet, mais également la manière dont il réagit à l'éclairage, son degré de transparence, sa réflectivité éventuelle.
Le matériau, c'est d'abord la couleur de l'objet. Mais le matériau peut aussi contenir une définition de texture 2D : une image «collée» à la surface de l'objet, ou encore une texture 3D ou texture procédurale, qui fait correspondre une couleur à un point de l'espace X,Y,Z.
Dans ce premier point nous allons énumérer les principaux types de surfaces qu’il est possible de représenter. La perception des surfaces dépend fortement de la nature des surfaces. Nous pouvons trouver des surfaces plus ou moins réfléchissantes, mais nous pouvons trouvez également des surfaces translucides, métalliques,...
Les principaux types de surfaces sont [Cou95]:
Les surfaces « Transparentes » :
Il s’agit de surfaces qui laissent pénétrer la plus grande partie des rayons lumineux et qui n’en réfléchissent que très peu.
Exemples : verre, eau, plastique,...
Les surfaces « Translucides » :
Il s’agit de surfaces qui ne laissent pénétrer qu’une partie des rayons lumineux et qui réfléchissent les autres. C’est le cas des verres translucides, de certains plastiques,...
Les surfaces « Opaques » :
Il s’agit de surfaces qui réfléchissent une partie des rayons lumineux incidents et qui en absorbent une autre. C’est le cas du carton, du bois,...
Les surfaces « Rugueuses » :
Il s’agit de surfaces qui réfléchissent la lumière dans toutes les directions. Elles ont ainsi un aspect mat et s’opposent à une surface lisse.
Les surfaces « Métalliques » :
Il s’agit de surfaces qui réfléchissent la couleur de la source lumineuse près de la normale à la surface et sa couleur propre quand on s’éloigne de celle-ci
Exemples : aluminium, inoxydable,...
Les surfaces « Miroirs » :
Il s’agit de surfaces qui réfléchissent parfaitement les rayons lumineux et qui possèdent uniquement la couleur de la source lumineuse qui l’éclaire.
Mais les surfaces des objets du monde réel n’appartiennent que rarement à l’une de ces catégories. Par exemple, le verre poli appartient a la catégorie des surfaces translucides et des surfaces opaques.
Lorsque l’on examine un objet du monde réel, on remarque également qu’il est affecté de nombreuses propriétés visuelles telles que la couleur, la texture, la transparence,... Ces deux premières propriétés seront expliquées par la suite.
Voici un bref descriptif des principales propriétés des objets :
La couleur :
Lorsque l’on regarde un objet du monde réel, une boule par exemple, on constate que les différentes parties de celle-ci a des couleurs différentes.
Ainsi on peut constater que la partie la plus éloignée de la source lumineuse a une nuance plus sombre : c’est la couleur Ambiante. Une tache blanchâtre est également visible du coté exposé à la lumière : c’est la couleur spéculaire. Les reste de la boule est d’une couleur intermédiaire : c’est la couleur diffuse.

La couleur de l’objet est donc définie par la combinaison de ces trois propriétés de la couleur.
La texture :
La texture est la représentation synthétique des matières et des arrangements de ses composants : grains des pierres, rainures du bois,...
Les textures permettent ainsi de donner un aspect plus réaliste aux surfaces.
La transparence :
La transparence est un facteur qui permet de déterminer le taux de transparence d’un objet. Au niveau 0, l’objet est opaque, au niveau 1 l’objet est complètement transparent.
La brillance :
La brillance est un facteur qui détermine la taille et l’intensité du reflet d’une surface. C’est-à-dire que la brillance détermine la vitesse d’atténuation de la lumière en fonction de son angle d’incidence avec la normale à la surface.
La rugosité :
La rugosité ou encore « réflectance » est le pouvoir réfléchissant d’une surface : ainsi un objet 100% rugueux réfléchira la lumière dans toutes les directions. Par contre, un objet lisse réfléchira la lumière symétriquement par rapport à sa normale.
La radiance :
La radiance ou « émission » détermine la lumière émise par la surface, indépendamment de toute source de lumière externe.
La réflectance :
La réflectance détermine la proportion de lumière incidente qui sera réémise par la surface.
Nous allons maintenant expliquer plus précisément les deux propriétés les plus courantes : les couleurs et les textures.
Comme expliqué plus haut, pour chaque matériau, vous définissez trois triplets de valeurs RGB .
Le diffus qui fixe la couleur de base du matériau.
L'ambiant qui fixe la couleur du matériau sous éclairage non direct.
Et enfin le spéculaire qui fixe la couleur du matériau à l'endroit d'un phénomène de brillance («highlight») : dans le cas de la sphère, c'est l'endroit où les rayons du spot frappent la surface perpendiculairement .
Exemple [L&M94]:
Supposons que les composantes RGB du diffus soient la couleur principale de l’objet .Vous pouvez adopter la règle de départ suivante : fixez les valeurs de l'ambiant à 50 % de celles du diffus, les valeurs du troisième à une teinte blanche ou gris moyen.
diffus 0,800 0,450 0,220
ambiant 0,400 0,225 0,110
spéculaire 0,400 0,400 0,400
Pour un matériau très contrasté (très sombre dans les parties non éclairées), diminuez les valeurs de l'ambiant.
Pour un matériau très brillant (chrome, plastique lisse) augmentez les valeurs du spéculaire à (1.0,1.0,1.0).
Voici le calcul le plus simple pour déterminer la couleur des faces, ce calcul ne tient pas compte des propriétés de rugosité, de transparence, de brillance de radiance ou de réflectance.
Ils ne tiennent pas non plus compte des algorithmes de lissage tels que « Gouraud »,...
Le calcul de la couleur ambiante :
La couleur ambiante est la couleur de l’objet en absence de lumière : dans ce sens, la face sera de couleur ambiante si la face n’est pas exposée aux rayons lumineux.
Pour savoir si une face est exposée à la lumière, il suffit de calculer si l’angle entre la direction de la lumière et la normale à la surface : si cet angle est supérieur à 90°, la surface n’est pas exposée à la lumière.
Le calcul de la couleur diffuse :
Le calcul de la couleur de la face exposée est plus compliqué : il ne suffit pas de donner la couleur diffuse à ces faces : la couleur des faces est fonction de l’orientation de la face.
Le calcul de l’intensité de couleur vue par l’observateur est fonction de l’angle (angle) formé par le vecteur passant par l’œil de l’observateur et le vecteur passant par la lumière incidente : [HIL90].
ID= angle * IS * RD
Où :
ID est l’intensité de la couleur diffuse, IS l’intensité de la source lumineuse et RD le coefficient de réflexion diffuse.
Le calcul de la couleur spéculaire:
Le calcul de l’intensité de la couleur spéculaire est différent :
Pour ce calcul, nous avons besoin de l’angle (Phi) entre l’œil de l’observateur et la direction dans laquelle la lumière est réfléchie.

Le calcul de l’intensité de couleur vue par l’observateur est fonction de l’angle (angle) formé par le vecteur passant par l’œil de l’observateur et le vecteur passant par la lumière incidente : [HIL90].
ISP= IS * RS * ( cos(F) )F(F)
Où :
ISP est l’intensité de la couleur spéculaire, IS l’intensité de la source lumineuse et RS le coefficient de réflexion spéculaire. F est une fonction qui associe une valeur entre 0 et 1 pour un phi allant de –90 à 90 degrés.

Cette fonction détermine le « falloff » de l’intensité de la composante spéculaire. Cette fonction est une courbe qui passe par (-90,0), (0,1) et (90,0) plus ou moins large selon la propriété de l’objet.
Dans la plupart des applications en images de synthèse, la couleur seule est insuffisante pour représenter de manière réaliste l’aspect des surfaces des objets de la scène. Une technique pour reproduire de manière plus détaillée les caractéristiques et irrégularités des surfaces, est de compléter l’habillage par la description des textures.
La texture 2D :
La texture dite 2D est un habillage de l'objet qui s'ajoute aux caractéristiques de base du matériau utilisé. Il s'agit de donner à tout l’objet ou à une partie de l'objet un aspect particulier : tissu de velours, plancher de bois, mur de briques.
Ce qui sert à cet habillage de l'objet n'est rien d'autre qu'une image en deux dimensions.
La texture peut être «collée» sur l'objet de manière à n'apparaître qu'une seule fois ou, au contraire, de manière à être répétée autant de fois que nécessaire.
Il existe habituellement quatre modes de collages ou de projections de la texture sur l'objet (mapping) selon la forme générale de l'objet à texturer : ces différents « mappings » sont essentiellement dus à la primitive qui sert à la projection.
la projection «orthogonale» où l'on projette chaque point de la texture perpendiculairement au plan dans lequel la texture est positionnée. La texture se dépose ainsi en quelque sorte à plat sur l'objet. Dans ce cas, certaines parties de l'objet se trouvent dans un plan non parallèle au plan de projection : à ces endroits la texture sera déformée proportionnellement à l'angle entre les deux plans.

la projection «cylindrique» où l'on projette chaque point de la texture à partir de l'axe central d'un cylindre.

la projection «sphérique» où l'on projette chaque point de la texture à partir du centre d'une sphère.

la projection «UV» où l'on projette la totalité de la texture sur la totalité d'une surface paramétrique. Les deux paramètres U et V du patch sont mis en correspondance avec les coordonnées X et Y de la texture.

Habituellement, pour éviter les effets d'additions de couleurs, on associe une texture avec un objet dont le matériau de base est blanc.
La texture 2D peut être utilisée non pas pour modifier la couleur d'une surface mais, plus subtilement, pour en modifier la luminosité. En pratique, la luminosité de la texture sert à perturber le calcul d'éclairement de la surface pour la rendre plus sombre ou plus claire.
On appelle cet effet le « bump mapping ».

Il existe une dernière technique qui consiste à interpréter un bitmap comme la transparence : un point blanc est considéré comme opaque et un point noir comme totalement transparent.
Cette technique permet par exemple de simuler un grillage devant un objet, elle permet d’économiser des milliers de polygones.
La texture 3D ou texture procédurale :
Les textures à 3 dimensions sont des algorithmes et non des images qui donnent à chaque point de l'espace une couleur qui ne dépend que de sa position.
Quand on dessine une surface avec ce type de texture, les coordonnées X, Y et Z de chaque point de la surface sont fournies à l'algorithme de texture 3D, qui détermine la couleur correspondante. Ces textures ne sont plus plaquées mais directement calculées par une fonction du type « pixel= couleur(x,y,z) ».

On réalise en textures 3D des surfaces d'aspect bois, marbre, pierre, fibres, etc... sans avoir de problèmes dans le cas des surfaces non développables.
Elles conviennent mieux pour les objets de formes complexes, mais ne permettent pas d'atteindre la même précision ni la même variété de détails que la méthode des textures 2D.
Maintenant que nous avons modélisé nos objets et leurs propriétés, nous pouvons dès à présent construire notre scène.
Mais afin de pouvoir visualiser quelque chose, nous devons placer des sources lumineuses afin d’éclairer la scène.
Ensuite nous devons définir une caméra virtuelle afin de modéliser l’œil de l’observateur : sa position, son angle de vue, direction,...
Enfin nous pourrons calculer le rendu de la scène qui est la représentation graphique du monde 3D composé de formes et sous formes numériques en « Pixel » qui seront affichées à l’écran ou sur tout autre support.
Lorsque nous voyons un objet, nous le percevons par ses couleurs intrinsèques et ses textures. Mais celles-ci ne peuvent que difficilement donner l’impression de volume et de relief aux objets de la scène. En effet, une sphère sans lumière donne un cercle de couleur uniforme : il manque un autre élément essentiel qui est l’éclairement.

Afin de reproduire aussi fidèlement que possible l’éclairage réel, on dénombre en général quatre grands types de sources de lumière :
La lumière ambiante :
La lumière ambiante éclaire toute la scène uniformément : elle ne provient pas d’une source particulière et ne possède pas de direction particulière : elle ne génère aucun reflet ni aucune ombre. En réalité, elle correspond à la lumière crépusculaire ou juste avant l’aube.
Lorsqu’elle est la seule lumière de la scène, elle génère des formes qui ne sont que des silhouettes planes et solides.
La définition de la lumière ambiante se fait par ses composantes RGB.
Pour son implémentation, le fait que cette lumière ne possède pas de direction entraîne qu’elle est considérée comme perpendiculaire à chaque face.
La lumière distante :
La lumière distante émet des rayons lumineux parallèles uniformes dans une seule direction. Ces rayons s’étendent à l’infini d’un coté ou de l’autre du point spécifié comme source lumineuse. Leur intensité est constante sur toute la longueur du rayon : chaque face reçoit la même intensité de lumière. Ce type de lumière est généralement utilisé afin de modéliser la lumière du soleil : on considère que ses rayons sont parallèles.
Pour son implémentation, chaque face est traitée de la même manière :
ID= cos(angle) * IS * RD
Où : ID est l’intensité de la couleur diffuse, angle est l’angle entre la direction des rayons et la normale à la face, IS l’intensité de la source lumineuse et RD le coefficient de réflexion diffuse.

Cette formule ne tient pas compte des reflets : pour plus d’informations, le lecteur peut se référer au livre de F.S. HILL : «Computer Graphics» pg 643. [HIL90]
La lumière ponctuelle :
La lumière ponctuelle émet de la lumière dans toutes les directions : elle est généralement utilisée pour modéliser la lumière d’une ampoule, d’une flamme,..
Son calcul s’effectue de la même manière que pour la lumière distance avec la différence que la direction de la lumière n’est plus constante et que l’intensité de la source diminue avec la distance entre le point lumineux et la surface(« déperdition »).
Il existe habituellement deux techniques pour le calcul de la « déperdition » L’inversion linéaire ou l’inversion du carré de la distance.

La lumière dirigée :
La lumière dirigée est destinée à modéliser des sources lumineuses de type projecteurs , lampes de bureaux, phares de voitures,...
Elle est constituée d’un cône de lumière directionnel. La définition d’une telle source de lumière se fait par la définition de son cône : on définit la direction principale du cône et son angle d’ouverture.
En général on définit un deuxième spot dont l’intensité est moindre et l’angle d’ouverture est supérieur : cette deuxième lumière superposée à la première sert à modéliser le « FALLOFF » ou zone de pénombre entourant en général un spot.
Ce type de lumière est une restriction de la lumière ponctuelle.

En général l’éclairage d’une scène est composé de plusieurs sources lumineuses qui appartiennent à ces différents types : pour chaque face, il faut tenir compte de toutes les lumières présentes dans la scène et de leurs propriétés.
Comme en photo, l'ordinateur utilise les lois de l'optique pour réaliser des images réalistes. Nous imaginerons donc que l'écran de visualisation est une fenêtre sur laquelle on va projeter une image ou une partie de l'image. Cette fenêtre peut être interprétée comme la rétine de l’œil de l’observateur ou de la pellicule dans le cas d’une caméra réelle.
Si ce monde est bidimensionnel, peu de problèmes se posent. Si, par contre, comme le monde réel, le monde virtuel est en 3 dimensions, nous effectuons donc une projection des entités géométriques du monde pour en faire des entités à 2 dimensions dans le plan de l'image.
Deux grands types de projections sont généralement utilisés : la projection parallèle et la projection perspective.
La projection parallèle :
Cette technique de représentation consiste à projeter parallèlement la scène sur la fenêtre de visualisation en conservant sa forme et ses proportions.
Cette méthode est particulièrement utilisée dans le cas du dessin technique.

La projection perspective :
La technique de projection perspective ne conserve plus les proportions strictes de la forme mais tel qu'elle apparaît à l'œil de l'observateur. Les objets représentés en perspective sont caractérisés par un effet de "raccourci" et par l'existence de points de fuites. Cette méthode est largement utilisée en synthèse d'images.

La caméra peut être considérée comme faisant partie du monde virtuel qu'elle regarde.
Cette façon de considérer le système permet au programmeur de manipuler les points de vue en ne modifiant en rien la géométrie du monde observé, et aussi de modifier un élément de ce monde sans perturber le point de vue.
La caméra que nous allons considérer est une caméra réalisant une projection perspective : cette caméra est l’analogue de la caméra réelle.
La configuration de la caméra implique une prise en compte des paramètres suivants .
La distance focale : par analogie avec la caméra réelle la distance focale est la distance entre la lentille de celle-ci et la pellicule. Les distances les plus utilisées vont de 15 à 200 mm. Une distance de 50 mm correspond à une vision normale de l’œil humain (approximativement D dans l’équation précédente).
Le champ de vue : il s’agit de l’angle de vision couvert par l’objectif. Le champ de vue et la distance focale sont étroitement liés : une distance focale « courte » équivaut à un grand angle, une focale « longue » équivaut à un champ de vue étroit.
La profondeur de champ : la profondeur de champ peut être définie comme une zone de netteté qui s’étend du premier plan du sujet, passe par le plan de mise au point et finit à l’arrière-plan [Cou95].
En général, la caméra est définie différemment en images de synthèse, le concept de focal reste : il est traduit soit par la distance du centre de projection et le plan de la fenêtre (window) de visualisation de la scène, soit par l’angle de vue.

Image extraite de [HIL90]

En général, pour définir la position et la direction de la vue ou caméra virtuelle on donne la position (x,y,z) de celle-ci (PROJECTION CENTER), un vecteur unitaire qui donne la direction, le sens de l’axe de la caméra ou axe de visée et un vecteur vertical à cet axe qui donne la direction du haut. Ce dernier vecteur permet de définir l’angle de rotation autour de son axe de visée. Le plus souvent, ce dernier vecteur est remplacé par deux vecteurs U et V qui donnent respectivement les axes X et Y du plan de projection.
La profondeur de champ, quant à elle, est remplacée par un plan (FAR) au-delà duquel les objets ne son plus dessinés et un plan (NEAR) à partir duquel les objets sont dessinés. La définition de ces deux plans perpendiculaires à l’axe de visée de la caméra virtuelle et la définition de la position de la caméra permet de définir un volume (VIEW VOLUME) au sein duquel les objets sont dessinés et pas les autres.
Avec la librairie OpenGL™ par exemple, la définition de la vue se fait en deux phases, une première qui définit les paramètres de la vue : distances aux plans NEAR et FAR et l’angle de vue et une deuxième phase qui définit la position et la direction (+ sens) de l’axe et la direction du haut de la caméra.
Maintenant que nous avons défini les concepts de base d’une caméra, nous pouvons nous intéresser aux différents types de caméras.
Une partie des recherches effectuées pour ce mémoire s’est portée sur la caméra virtuelle : ces recherches ont abouti à la définition de différents types de caméras et leur implémentation dans une animation temps réel 3D.
Nous allons d’abord définir à quel moment il faut placer la caméra..
Nous allons ensuite définir les différentes caméras ainsi que donner l’implémentation de celles-ci dans un langage graphique OpenGL™.
Enfin, nous donnerons des exemples où ces différentes caméras peuvent être utilisées.
Le lecteur qui désire en savoir plus sur l’implémentation de ces différentes caméras peut se référer au programme « Solar ». Cette application à été implémentée afin de montrer la différence entre ces caméras. Elle représente le système solaire parcouru par un vaisseau spatial : cette scène peut être regardée avec les différentes caméras et celles-ci peuvent être déplacées et orientées dans l’espace. Le fichier « Caméra.cpp » contient l’implémentation OpenGL™ dans un objet de ces différentes caméras.
Lors de la configuration de la caméra, le plan de projection et le volume de l’espace qui est vu est défini. Cette définition de la vue doit, pour l’animation temps réel être définie avant toutes primitives d’affichage : en effet, chaque objet est dessiné à l’écran en fonction de la position de la caméra.
Il convient donc de définir les paramètres de la caméra avant la première image de l’animation : nous pouvons donc définir la distance des plans NEAR et FAR par rapport au plan de projection (WINDOW), la largeur de la vue (focal) et la taille de la fenêtre de visualisation.
Ces paramètres ne sont, en général, plus modifiés pour le reste de l’animation.
Une fois ces paramètres fixés, nous pouvons nous intéresser au positionnement et à l’orientation de la caméra.
Il est en effet beaucoup moins rare dans une animation d’user de « traveling » ou de vue panoramique.
Avant chaque image il faut alors positionner et orienter la caméra. La définition de la position et de l’orientation de la caméra équivaut à la définition du plan de projection.
Une fois ce plan de projection défini, on peut alors définir le volume de l’espace qui sera projeté.
Enfin, nous pouvons utiliser un algorithme de rendu pour afficher la scène.
Les types de caméras qui vont suivre se basent sur la définition du positionnement et de l’orientation de la caméra avant l’affichage. Les algorithmes qui vont suivre partent du principe que les paramètres fixes ont déjà été définis (NEAR,FAR, focale) et que la caméra est placée par défaut au centre du monde virtuel, en (0,0,0), dirigée vers l’axe des Z croissant et les axes sont X (U) et Y (V) de la caméra sont confondus avec les axes X et Y du monde virtuel.
Le principe général de ces caméras est assez simple : effectuer des translations et des rotations sur les valeurs par défaut, qui ont été définies ci-dessus afin d’obtenir la caméra voulue. Les rotations autour de l’axe des Z, par exemple, permet à la caméra de tourner autour de son axe de visée.
Dans son implémentation avec la librairie OpenGL™ , cette caméra est définie comme une suite de transformations appliquées directement après la définition de la perspective (NEAR,FAR et focale ). Ces transformations sont alors répercutées à toutes les primitives qui suivent.
La caméra libre :
La première caméra est la plus simple : c’est une caméra qui est positionnée en un point (x,y,z) de l’espace et qui est orientée suivant une direction arbitraire définie par des angles autour des trois axes.
C’est une caméra qui est totalement libre de tous ses mouvements.
Voici l’implémentation d’une telle caméra ( en primitives OpenGL™ ).
L’ordre des opérations ayant une conséquence sur le résultat, nous allons d’abord définir les transformations qui orientent l’axe de visée de la caméra et juxtaposent ses axes U et V sur les axes de la fenêtre de visualisation (VIEWPORT ». cette opération s’effectue par une rotation autour de chaque axe de la caméra par défaut (Angx, Angy et Angz).
Ensuite nous déplaçons la caméra vers sa position dans l’espace virtuel (X,Y,Z).
glRotatef( Angx, 1.0 ,0.0 ,0.0);
glRotatef( Angy, 0.0 ,1.0 ,0.0);
glRotatef( Angz, 0.0 ,0.0 ,1.0);
glTranslatef( -X, -Y, -Z);

La caméra embarquée :
La deuxième caméra n’est plus totalement libre, Elle fixe un point et se positionne en fonction de celui-ci.
Entre autre, c’est la caméra qui suit un objet en mouvement et qui effectue les mêmes mouvements : c’est par exemple la caméra embarquée dans une voiture en mouvement et qui filme le rétroviseur.
Mais elle peut également être la caméra qui tourne autour d’un objet en mouvement : cette caméra n’est pas fixée physiquement à l’objet , comme l’est souvent la caméra embarquée réelle. Elle peut se rapprocher de l’objet ou encore tourner autour de celui-ci.

Nous allons introduire un nouveau concept, le point de référence : le point de référence est le point qui est fixé par la caméra, il se situe sur l’axe de visée de la caméra. Ce point de référence peut par exemple être le centre de l’objet que la caméra regarde.
Ce point de référence a pour effet de fixer l’axe de la caméra sur la droite qui passe par ce point et par le point où se situe la caméra.
L’introduction de ce point de référence limite les mouvement de la caméra : elle ne se situe plus arbitrairement dans l’espace mais elle se situe à une certaine distance du point de référence. Elle peut également s’orienter dans toutes les directions Mais les rotations qui permettent cette opération ne se font plus autour de ses propres axes (repère local propre à la caméra), elles se font autour des axes du point de référence (repère local du point de référence).
Voici l’implémentation de la caméra embarquée (en primitives OpenGL™ ).
Nous allons tout d’abord éloigner la caméra du point (0,0,0) du repère globale de la scène à une distance R (suivant l’axe des Z) : est la distance entre la caméra et le point de référence.
Ensuite nous allons orienter la caméra par des rotations autour des axes du repère globale de la scène(Angx, Angy et Angz).
Le point de référence est encore le point (0,0,0) du repère globale : nous allons donc effectuer une translation afin d’amener ce centre du monde sur le point de référence (X,Y,Z).
glTranslatef ( 0.0, 0.0, -R);
glRotatef ( Angx, 1.0, 0.0, 0.0);
glRotatef ( Angy, 0.0, 1.0, 0.0);
glRotatef ( Angz, 0.0, 0.0, 1.0);
glTranslatef ( -X, -Y, -Z);

La caméra « intelligente » :
La caméra « intelligente » est une caméra qui se positionne arbitrairement dans l’espace et qui s’oriente automatiquement vers un point de référence. Elle peut par exemple servir à modéliser la vision d’un personnage en mouvement qui suit des yeux une voiture qui passe dans la rue.
Le terme « intelligent » vient du fait que la caméra s’oriente en fonction du point de référence et de sa propre position.

Deux possibilité s’offrent pour l’implémentation de cette caméra .
Soit positionner en premier la caméra sur sa position finale et ensuite l’orienter vers le point de référence.

Soit orienter d’abord la caméra et ensuite positionner la caméra à sa place.

La première implémentation semble la plus logique mais c’est la deuxième qui a été retenue.
On peut se dire à priori que le temps de calcul pour ces deux caméras est identique : une conversion de coordonnées cartésiennes en coordonnées sphériques pour définir les angles pour l’orientation et un déplacement de la caméra.
Mais la rotation s’effectue toujours autour du centre du monde (des axes du repère global) : si une caméra déjà positionnée en (x,y,z) (¹ (0,0,0)) est ensuite orientée, le résultat serait semblable au résultat obtenu avec la caméra embarquée. Il faut donc la ramener sur le centre du monde (0,0,0), l’orienter et la repositionner en (x,y,z).
Dans ce cas la première implémentation reviendrait à positionner la caméra, à la ramener sur le centre du monde et appliquer les transformations de la deuxième implémentation.
De plus, la ressemblance au point de vue transformation de la caméra « intelligente » et de la caméra libre permet de passer sans calcul (de l’orientation) du type caméra « intelligente » à une caméra de type libre.
La seule différence entre ces deux caméras est que pour la caméra « intelligente » l’orientation n’est plus arbitraire mais est fonction des positions respectives du point de référence et de la caméra.
Le principe de base de l’algorithme est simple, on calcule le changement de coordonnées (cartésiennes à sphériques) de la différence entre les deux positions (caméra et point de repère). On obtient ainsi l’orientation et la distance entre la caméra et le point de référence (R). Ensuite on oriente la caméra et on la positionne en (x,y,z).
Voici l’implémentation en primitives OpenGL™ de la caméra « intelligente ».
Remarques :
les variables Refx, Refy et Refz correspondent à la position (x,y,z) du point de référence.
les variables Posx, Posy et Posz correspondent à la position (x,y,z) de la caméra.
On fixe Angz (angle de rotation de la caméra autour de son axe de visée)
Dx = ( Pos.x - Ref.x);
Dy = ( Pos.y - Ref.y);
Dz = ( Pos.z - Ref.z);
/*changement de coordonnées */
On calcul Angx et Angy en fonction de la position (Dx,Dy,Dz)
glRotatef ( Ang.x, 1.0, 0.0, 0.0);
glRotatef ( Ang.y, 0.0, 1.0, 0.0);
glRotatef ( Angz, 0.0, 0.0, 1.0);
glTranslatef( Posx, Posy, Posz);
Ces trois types de caméras ne se retrouvent dans la réalité que par l’action du cameraman et des moyens techniques extérieurs à cette caméra c’est-à-dire des mouvements de celle-ci..
Il est évident que ces caméras peuvent modéliser n’importe quels mouvements d’une caméra réelle mais ces trois types de caméras sont mieux adaptés à certaines modélisations :
La caméra libre peut être utilisée pour modéliser une caméra fixe qui filme une pièce de théâtre. Elle peut être utilisée comme une caméra qui filme en panoramique un paysage. Mais elle peut également modéliser la vision d’un observateur lorsqu’il bouge la tête(orientation) en marchant(position).
La caméra embarquée peut modéliser une caméra physiquement liée à l’objet qu’elle filme comme, par exemple, les caméras fixées à la carrosserie d’une voiture qui filme le conducteur à travers le pare-brise.
La caméra « intelligente » permet de modéliser les mouvement du cameraman qui filme un objet en mouvement. Comme, par exemple, les poursuites : la vision du policier qui poursuit la voiture. Cette caméra permet de modéliser les mouvements de la tête que nous faisons instinctivement lorsque nous suivons du regard un objet en mouvement.
Maintenant que nous avons modélisé nos objets, que nous avons placé nos lumières et notre caméra, nous pouvons calculer les faces ou parties de faces des objets qui seront vues.

Cette opération s’appelle le calcul du vu et caché ou élimination des faces cachées.
La plupart des objets que nous voulons visualiser sont opaques. De ce fait, seules les faces frontales seront vues. Toutes les faces qui seront masquées par une autre face ne seront pas affichées, il en est de même pour les parties de faces masquées.
Il existe beaucoup d’algorithmes d’élimination des faces cachées, certains demandent plus de mémoire, d’autre plus de temps de calculs, d’autres encore ne s’appliquent qu’à certains types d’objets. Il faudra dès lors choisir une combinaison d’algorithme en fonction des besoins ou de l’équipement
Un travail préliminaire peut être effectué indépendamment de l’algorithme choisi, l’élimination des faces orientées dans une direction opposées à la caméra (BACK-FACE), afin de diminuer le nombre de faces à prendre en considération.
Ce travail est assez simple à mettre en œuvre : il suffit de calculer la normale (tournée vers l’extérieur de l’objet ) à la face et de regarder si l’angle formé par cette normale et la direction de la vue en ce point est supérieure à 90 degrés : si c’est le cas, la face ne sera pas vue. Autrement dit, si la normale à la face a une composante suivant la direction de la vue.
Une fois ce tri effectué, nous devons utiliser un algorithme de vu et caché car cet algorithme d’élimination ne convient que si la scène ne comporte qu’un objet convexe et que la projection utilisée est orthogonale.
Les algorithmes de vus et cachés sont généralement classés en deux grandes [HIL90] : les algorithmes qui travaillent dans l’espace objet et ceux qui travaillent dans l’espace image.
Les méthodes de vus et cachés de l’espace objet sont des algorithmes qui utilisent les positions X, Y et Z de l’espace virtuel 3D pour définir les faces ou morceaux de faces qui seront affichés.
En opposition, les méthodes dans l’espace image utilisent les positions X et Y obtenues après la projection de 3D vers 2D de la scène.
L'algorithme du peintre :
C'est une méthode de vu/caché par tri préalable (back to front sorting).
Elle consiste à garder triées les entités géométriques par ordre de leur distance à la caméra. Ce tri peut s’effectuer dès que la position de la caméra est fixée, on peut alors déterminer la distance des faces et les trier.
Ensuite on affiche à l'écran les faces les plus lointaines pour commencer, on les cache successivement en dessinant «par-dessus» les faces les plus proches.
La routine d'affichage n'a alors plus aucun effort à consentir pour que l'image soit « correcte ».
Evidemment, tout changement de point de vue oblige à modifier l'ordre d'affichage. Cette méthode convient donc bien pour des modèles fixes vus d'un point de vue fixe.
Cet algorithme ne donne pas toujours de bons résultats : si les faces se recoupent, l’algorithme ne sait pas résoudre les problèmes d’intersections.
Mais le problème majeur de cet algorithme est la détermination de la distance d’une face : si la face est parallèle au plan de projection, tous les points on la même distance mais pour les autres il faut calculer par exemple la distance du point central de la face : ce qui peut occasionner des erreurs.
L’utilisateur désirant plus d’informations sur cet algorithme peut se référer au projet de première licence de l’année académique 1995-1996 « Représentation et animation de fonctions de deux variables en trois dimensions », au livre de F.S. HILL « Computer Graphics ». [HIL90]
Le plan de séparation :
Cette méthode de vu/caché espace objet trouve son intérêt dans les scènes à objets multiples.
Si nous plaçons un plan imaginaire entre deux objets de la même scène, nous pouvons utiliser l'équation du plan pour savoir de quel côté est la caméra, et ainsi déterminer quel objet est du bon côté du plan et doit donc être affiché en dernier lieu.

Il suffit d'avoir les équations d'un certain nombre de plans séparant les divers objets à afficher pour pouvoir les trier.
Cette méthode convient bien et est assez simple pour des simulateurs de véhicules routiers. Les plans de séparation entre les bâtiments sont dans l'axe des routes et peuvent être calculés à priori.
Le tri en profondeur de champ :
L’algorithme de tri en profondeur est assez simple .
On projette les faces de la scène sur des plans perpendiculaires à l’axe de visée de la caméra. On ne projette que les objets ou parties d’objets définis entre le plan sur lequel on projette et le précédent (si c’est le premier plan, le précédent est le plan FAR défini plus haut).
On affiche ces plans par ordre de distance à la caméra décroissant.

Cette technique est utile dans les scènes à objets multiples se recouvrant partiellement. Cette méthode est d'autant plus facile à appliquer que les objets à afficher sont plans faciles à projeter sur des plans transversaux.
Cet algorithme engendre quelques problèmes : la qualité de l’algorithme est proportionnel au nombre de plans considérés : il faut, pour avoir un bon résultat, avoir des plans espacés d’au maximum la différence de profondeur entre le sommet le plus éloigné et le plus près de la face.
La place occupée en mémoire par ces plans de projections est énorme.
La décomposition :
Cette méthode de vu/caché espace objet est utilisée pour les objets modélisés par une méthode volumique qui décompose le volume de l'objet modélisé en volumes élémentaires
Pour afficher ce type d'objet correctement, il suffit d'afficher les sous-éléments (les cubes élémentaires) les plus lointains en premier lieu avec l'algorithme du peintre par exemple.
Le lecteur qui désire plus d’informations sur cette méthode peut se référer au livre « Computer Graphics » de D. HEARN et Pauline BAKER. Pg 270. [H&B86].
Le Z-Buffer :
Comme son nom l’indique la méthode du Z-Buffering est de tenir à jour un buffer contenant les positions Z (suivant l’axe de visée de la caméra ) de tous les points de la fenêtre de visualisation.
On projette face par face les objets de la scène : si à l'emplacement du pixel à afficher, une valeur Z existe déjà, on compare cette valeur à la valeur Z du nouveau pixel.
Si la valeur Z du nouveau pixel que l'on ajoute est supérieure à celle du pixel déjà affiché à cette même place, c'est qu'il est plus proche de l'observateur.
On affiche donc le nouveau pixel à l'écran et on met à jour le Z-Buffer. Dans le cas contraire, le pixel déjà présent est conservé et le Z-Buffer n'est pas modifié.
Cette méthode est correcte dans tous les cas, quelle que soit la complexité de la scène, le nombre et les positions relatives des objets, etc...
Malheureusement, elle coûte cher en temps de calculs et en espace mémoire, sauf dans les cas où elle est implantée dans le hardware de la machine : dans de nombreuses stations de travail (notamment la plupart des machines Silicon Graphics les cartes graphiques MGA Millenium et Mystique), le Z-Buffer existe dans la partie câblée de la carte d'affichage écran.
Il n'est pas indispensable que cette fonction soit câblée car elle peut aussi être réalisée de façon logicielle. Si la table possède une précision de 16 bits par valeur Z, il est nécessaire de consacrer au Z-Buffer une taille de 2 octets par pixel (soit 614.400 octets pour un écran de 640×400 pixels, ou 128.000 octets pour un écran de 320×200 pixels) [L&M94].
Il convient de bien choisir à quelle distance en Z correspondent les minima et maxima des valeurs stockées dans le Z-Buffer pour garder une bonne précision dans les intersections d'objets.
Si de nombreux objets presque parallèles au plan de l'écran se coupent, une précision importante est nécessaire pour éviter les artefacts (effet indésirable d’escalier). Il faut alors réduire la profondeur de la zone utile du Z-Buffer ou lui consacrer un nombre élevé de bits par pixel.
Le lecteur qui désire plus d’informations sur cette méthode peut se référer aux livres :
« Computer Graphics » de F.S. HILL. Pg 595. [HIL90]
« Computer Graphics » de D. HEARN et Pauline BAKER. Pg 262 [H&B86].
Scan-line :
Cette méthode de vu/caché dans l'espace image est directement dérivée de la méthode Z-Buffer.
Dans ce cas-ci, on ne mémorise pas une table de Z pour tous les pixels de l'écran, mais seulement pour tous les pixels d'une ligne horizontale de l'écran.
L'image est alors calculée ligne par ligne : pour chaque polygone à afficher, on cherche d'abord s'il coupe l'horizontale correspondant à la ligne de l’écran en cours.
Si oui, on agit comme dans le cas du Z-Buffer. Cette stratégie est appliquée pour chaque ligne de l'écran à tous les polygones de la scène à afficher.
Cette méthode est plus pénalisante en temps de calcul que la méthode Z-Buffer, mais elle demande beaucoup moins d’espace mémoire.
Le lecteur qui désire plus d’informations sur cette méthode peut se référer aux livres :
« Computer Graphics » de F.S. HILL. Pg 597. [HIL90]
« Computer Graphics » de D. HEARN et Pauline BAKER. Pg 264. [H&B86]
Le Minimax :
C’est une technique qui teste si les objets peuvent se chevaucher ou non : on englobe les objets par des formes rectangulaires (dans le plan de projection) et on vérifie si ces rectangles se recoupent : ce test est rapide car il ne doit tester que les minima et maxima des rectangles.

Comme on le voit dans la figure, les valeurs minimales et maximales des coordonnées X et Y de deux rectangles englobant les objets sont analysées pour vérifier s'il y a risque de recouvrement d'un objet par un autre.
Si le maximum en X d'un objet est plus petit que le minimum en X d'un autre objet, ils ne se cacheront pas l'un l'autre. On peut donc les dessiner dans n'importe quel ordre.
Si par contre, il existe un risque de conflit, on a recours à une autre des méthodes : comme, par exemple, le Z-buffer ou la Scan-line appliqués à la zone d’affichage qui pose problème.
Le Minimax permet, par un simple jeu de comparaisons, d'éliminer une part qui peut être non négligeable du temps de calculs demandé par ces algorithmes.
La solution optimale pour un problème donné est le plus souvent une combinaison des diverses méthodes.
En effet s'il existe des méthodes qui sont valables dans tous les cas, ce sont en général les plus lourdes à mettre en œuvre - le Z-Buffer, par exemple – sauf si cet algorithme est câblé dans le matériel graphique.
Un test de la complexité du cas permet souvent de choisir la méthode de complexité «juste nécessaire» à résoudre ce problème particulier.
Après avoir modélisé nos objets, placé nos lumières, notre caméra et défini les faces et parties de faces qui seront vues, nous pouvons enfin obtenir un rendu de la scène (« RENDER » en anglais) : la couleur de chaque pixel de la fenêtre de visualisation.
Beaucoup de méthodes de rendus existent : elles sont très différentes aussi bien en efficacité qu'en besoin de puissance informatique.
La puissance des processeurs n'est pas infinie et on se contentera donc d'utiliser l'algorithme « juste suffisant » pour le degré de réalisme que l'on désire obtenir.
Tous ces algorithmes déterminent la couleur d'un pixel affiché à l'écran. On utilise pour cela diverses informations comme l'orientation et la couleur de la face que l'on affiche, la couleur, l'orientation et la position des lampes éclairant la scène, la position d'un objet par rapport à l'autre, le matériau dont est constitué l'objet, sa texture, etc..
Nous allons maintenant passer en revue les différents types de rendus, du plus simple au plus compliqué, du moins réaliste au plus réaliste.
Le lecteur qui désire plus d’informations sur ces algorithmes de rendus peut se référer aux livres :
« Computer Graphics » de F.S. HILL. [HIL90]
« Computer Graphics » de Pauline BAKER et D. HEARN. [H&B86]
« La synthèse d’images. Du réel au virtuel » de J.P. Couwenbergh. [Cou95]

Le flat shading ou rendu «Lambert» fut historiquement le premier des algorithmes de rendu digne de ce nom. C'est aussi un des moins voraces en temps de calculs. Il fait intervenir un paramètre extérieur à l'objet à visualiser : la direction de la source de lumière.
Prenons comme hypothèse simplificatrice que nous n’avons qu’une source de lumière ponctuelle.
Pour chaque face des objets de la scène il va falloir calculer un vecteur unitaire qui donne l'orientation des rayons lumineux sur la surface plane que nous allons considérer.
Nous allons ensuite calculer une couleur qui dépendra de la couleur de l'objet et de l'angle d'incidence entre la normale au plan de la facette et le vecteur «éclairement».
On applique la loi de Lambert ou «loi du cosinus».
I = Ka *Ia +Kd *cos(i) *Ip.
Où :
I est l’intensité résultante.
Ka est un coefficient de réflexion de la lumière ambiante compris entre 0 et 1.
Ia est l’intensité de la lumière ambiante.
Kd est le coefficient de réflexion diffuse.
Ip est l’intensité de la lumière ponctuelle.
I est l’angle d’incidence de la lumière ponctuelle.
On fait ici diverses hypothèses, pas toujours très conformes à la réalité : la caméra est à l'infini et la facette est réellement la surface de l'objet et non son approximation.
La dernière hypothèse implique que l'on ait des variations brusques d'éclairement aux arêtes entre deux facettes voisines.
Cette formule est précisée dans le livre de D. HEARN et Pauline BAKER « computer Graphics » [H&B86] pg 276-282: vous pouvez y trouver la formule complétée pour les autres types de lumières et la position de l’observateur.
Le rendu « flat shading » est facile à calculer car il ne fait pas intervenir l’observateur.
L’aspect d’un tel rendu est plat et irréel c’est-à-dire mat et sans reflet.
La méthode de Gouraud (Henri) permet d'obtenir le rendu d'une face avec un aspect «lissé» c’est-à-dire sans qu'il n’y ait de variations soudaines de couleurs ou de luminosité entre deux facettes contiguës.
Lors de l'affichage des pixels correspondant à une face, on détermine la couleur de la facette en chacun de ses sommets : on calcule la somme vectorielle des normales aux facettes contiguës à ce sommet et on la norme. On calcule ensuite la couleur de chacun des sommets de la face (de la même façon que dans le « flat shading »).
Ensuite, on calcule une double interpolation linéaire entre ces couleurs pour obtenir la couleur d’un point particulier de la face.

Premièrement, on calcule la couleur pour les sommets S1, S2, S3 et S4.
Ensuite on calcule la couleur de I1 et I2 par une interpolation linéaire de respectivement S1, S4 et S2, S3.
Ensuite on obtient la couleur de P par interpolation linéaire de I1 et I2.
On peut facilement vérifier qu'il n'y ait pas de discontinuité dans les teintes entre deux facettes adjacentes : dans les deux facettes qui partagent une arête commune, les couleurs aux extrémités sont identiques car elles dépendent uniquement des normales précalculées en ces deux points.
Les pixels intermédiaires de l'arête sont bien identiques sur les deux facettes, car obtenus de la même façon par une interpolation linéaire entre les couleurs des deux sommets.
Le résultat donne des réflexions relativement distribuées et douces mais présente également quelques inconvénients :
Les facettes traitées doivent être convexes.
Les effets de la réflexion spéculaire ne sont pratiquement pas reproduits, ce qui enlève tout aspect brillant aux objets.
La couleur obtenue dépend de l’orientation des facettes, ce qui peut provoquer des défauts visibles en cas d’animation de la scène.
Les stations de travail professionnelles bénéficient de plus en plus souvent d'une implémentation matérielle de cet algorithme. Ils effectuent généralement cet ensemble de calculs pour un certain nombre de sources de lumières qui peuvent être colorées (composantes R, G et B différentes), et situées à des distances finies.

L'algorithme de Phong est bâti sur la même base que celui de Gouraud, mais au lieu d'interpoler les valeurs de couleurs obtenues, on interpole les directions des normales pour obtenir une normale à l'objet en chacun des pixels que l'on veut afficher.
Le calcul est donc plus correct, mais nécessite environ cinq à dix fois plus de puissance de calcul.
Le résultat est nettement meilleur qu'avec la méthode Gouraud pour les objets brillants ou métalliques, notamment pour les reflets provoqués par des sources de lumière proches.
La méthode de phong a été retenue pour les implémentations car elle apporte un mode de visualisation idéal pour les séquences animées car elle offre une qualité d’image très satisfaisante et un temps de calcul encore raisonnable.

Les méthodes que nous allons voir maintenant utilisent des modèles d’éclairements globaux qui permettent de créer des images d’une qualité bien supérieure car il tiennent compte de tous les phénomènes optiques en présence : réflexion, réfraction, ombrage, transparence, ...
Malheureusement la prise en compte de tous les éléments se traduit par un temps de calcul considérable.
Le « Ray-Tracing » fait appel à un algorithme très particulier issu des recherches faites dans le domaine des radiations nucléaires : le « lancé de rayons ».
Cette technique est certainement une des plus efficaces et une des plus complètes pour générer des images réalistes, mais aussi une des plus gourmandes en temps de calcul.
Elle permet de prendre en compte :
La position de l’observateur et des sources lumineuses.
L’élimination des parties cachées.
Les phénomènes de réflexion, réfraction et transparence.
La réflexion des objets les uns sur les autres.
Le calcul des ombres et ombres portées (ombres d’un objet sur un autre).
Le traitement d’anti-aliasing.
Le « lancé de rayons » part du principe que l’image qui arrive à la caméra est la somme des rayons en provenance des diverses sources lumineuses et leurs multiples déviations et diffractions sur les objets et de leurs transformations en fonction des caractéristiques de ces objets.
Le principe de son algorithme est analyser le trajet inverse des rayons lumineux atteignant l’observateur ( on se limite aux rayons qui arrivent sur la matrice des « pixels » de l’écran).
Pour chaque « pixel » de la fenêtre de visualisation, ont retrace le trajet d’un rayon lumineux partant de l’œil (il est fixé pour le calcul) et passant par celui-ci.

Chaque fois que l'on trace un rayon, il faut calculer son intersection éventuelle avec toutes les facettes de la scène.
Lorsque ce rayon rencontre un objet, on applique les lois de la réflexion et de la réfraction : le rayon reflété est dévié et il convient de calculer cette déviation afin de continuer à remonter la trajectoire.
Si l’objet est transparent, le rayon se subdivise en un rayon réfléchi et un rayon réfracté : ces deux rayons doivent être suivis.
On continue ce processus jusqu’à ce que le rayon arrive à une source lumineuse.
On peut également définir une distance maximale des rayons afin de stopper le calcul des rayons inverses qui n’aboutissent pas à une source lumineuse.
Les rayons qui passent par une source de lumière prendront les caractéristiques de cette source. Les rayons provenant du fond de la scène(trop loin) seront soit noirs, soit prendront la couleur du «ciel», c'est-à-dire une couleur de fond fixée à priori.
Pour déterminer l’intensité finale de chaque « pixel », on calcule l’intensité totale transmise à l’œil pour tous les rayons provenant des sources et passant par ce « pixel ».
En respectant les lois de l'optique, on réalise ainsi des images fort réalistes d'objets divers, même transparents ou translucides. Il suffit de tenir compte lors des réflexions et réfractions des rayons des paramètres réels de transmission, comme transparences à diverses couleurs, indice de réfraction et même taux d'opacité.
Les algorithmes de Ray Tracing impliquent une quantité de calculs absolument phénoménale.
Par contre :
Les deux opérations de rendu et de détection de visibilité y sont intrinsèquement liées.
Le calcul des ombres est d'office inclus dans ce même procédé.
La plupart des algorithmes de ce genre limitent le nombre de réflexions prises en compte. Malgré ce genre de limitations, le calcul d'une image peut durer entre plusieurs heures et plusieurs jours pour des scènes complexes.
Ces algorithmes donnent de très bons résultats quand les surfaces réfléchissent beaucoup de lumière : miroirs, métaux polis, verre,...
Le lecteur qui désire en savoir plus peut se référer au livre « Computer Graphics » de F.S. HILL (pg 615-670) [HIL90]. Les programmeurs intéressés par du code source en langage C doivent se procurer le programme « RayShade » (« freeware »).

C’est une technique dérivée de la thermodynamique. Elle a été mise au point à l’Université Cornell en 1984.
La radiosité est une méthode de rendu qui calcule les couleurs des objets en résolvant les équations d'échange de rayonnement lumineux entre les diverses surfaces de la scène soumises à des éclairages. C’est-à-dire qu’elle calcule la somme des rayons lumineux frappant un point d’une surface en fonction de l’intensité issue de chaque autre élément de la scène.
Les équations de radiosité sont complexes et leur résolution n’est opérationnelle (temps de calcul) que pour les lumières diffuses.
La radiosité permet de prendre en compte l’interaction des réflexions diffuses des objets entre eux. Elle permet un traitement plus réaliste des ombres et est indépendante du point de vue.
Malheureusement elle ne permet pas à elle seule de traiter la réflexion spéculaire.
La radiosité est intéressante dans un cas précis. Les calculs d'éclairages étant indépendants de la position de la caméra virtuelle, la méthode est idéale pour le « walk-through » en architecture. Un seul calcul d'éclairement suffit tant que ni les objets ni les lampes ne bougent.
Maintenant que nous pouvons créer et visualiser une image de synthèse, nous pouvons créer l’illusion du mouvement.
Pour donner l’illusion du mouvement il faut présenter les images successives à une cadence élevée (minimum 25 par seconde) que l’œil humain ne puisse pas détecter la succession d’images mais un mouvement continu.
Dans cette partie, nous allons nous intéresser aux mécanismes qui permettent de modifier les objets ou ensembles d’objets afin d’obtenir les images fixes, la succession de ces images donnera alors l’illusion de mouvement des objets.
L’interprétation de « modifier un objet » doit être prise au sens large : il peut s’agir de mouvements (translations, rotations), de déformations (dimensionnement, pliage courbe,...), de changement de propriétés (textures, couleurs, luminosité,...) sur n’importe quel élément de la scène (objets, lumières, caméra).
Ces méthodes sont en général coulées entre elles pour offrir à l’utilisateur un plus large éventail de possibilités afin de représenter le plus fidèlement les mouvements réels.
Le lecteur qui désire obtenir plus d’informations sur ce sujets peut se référer aux livre de J.P. Couwenbergh « la synthèse d’images, du réel au virtuel » [Cou95] ou au CD-ROM « 3D Animation » de Neurone production.
Ce mécanisme est basé sur la technique utilisée pour le dessin animé traditionnel : dans le dessin animé traditionnel , il existe deux métiers distincts : celui d'animateur et celui d'intervalliste. L'animateur dessine les positions clés d'un mouvement et l’intervalliste complète ensuite le mouvement en dessinant les positions intermédiaires manquantes.
L’animation par scènes clés sur ordinateur est une extension de cette méthode traditionnelle : l’utilisateur joue le rôle de l’animateur et l’ordinateur celui de l’intervalliste.
L’utilisateur définit les scènes principales en plaçant et modifiant les objets, les lumières et la caméra. L’ordinateur quant à lui se charge de calculer les images intermédiaires.
Le calcul dans la technique des scènes clés se base sur une interpolation linéaire ou à base de Splines.
L’interpolation linéaire génère des déplacements linéaires faciles à calculer : cette technique est peu réaliste.
Prenons par exemple une balle qui rebondit sur le sol : si nous utilisons trois scènes clés chronologiques en bas, en haut et en base (déplacer dans une direction horizontale). L’animation donnera une balle qui monte en ligne droite et retombe en ligne droite.

Pour remédier à ce problème nous pouvons utiliser une interpolation à base de courbes Spline ou B-Spline.
Sur notre exemple, cette interpolation donne une trajectoire courbe qui ne tient pas comte des variations de vitesse.

Pour remédier à ce problème, nous pouvons utiliser une courbe avec contrôle de l’accélération et de la décélération.
Il existe également une autre méthode très proche qui consiste à définir d’abord la courbe de la trajectoire et ensuite d’interpoler les scènes clés sur la longueur de celle-ci : cette interpolation pouvant se faire en fonction des variations de vitesses. Cette technique est souvent appelée « l’animation par trajectoire ».
Cette technique d’animation est utilisée pour les mouvements de caméra dans le programme « MoleView » expliqué dans le chapitre suivant.
Cette technique permet de lier les modifications d’un objet à celle d’un autre. Le lien ainsi établi est dit « hiérarchique » dans la mesure où le premier objet contrôle le deuxième mais pas l’inverse. Il est courant d’utiliser une représentation en arbre de ces liens : un nœud « père » contrôle ses « fils » mais « un fils » ne contrôle pas son « père ».
Cette technique d’animation qui permet de définir la dépendance d’éléments par rapport à d’autres s’applique particulièrement bien aux structures articulées comme par exemple un bras ou une colonne vertébrale.
Dans le cas du bras, tout mouvement de l’avant-bras déplacé est répercuté à la main, aux doigts.
Il existe également plusieurs fonctions permettant un contrôle plus aisé des comme par exemple répercuter les transformations aux objets fils.
Par exemple on fait une rotation de 1 degré sur la première vertèbre, la deuxième hérite de la transformation de la première et effectue à son tour une rotation de 1 degré et ainsi de suite.
Pour le mouvement de structure articulée, on peut distinguer deux types de « cinématiques » :
La cinématique directe :
On répercute les transformations sur les objets fils et on réapplique à chaque fils la même transformation différente ou en fonction de la transformation du père.
Comme par exemple la rotation de la hanche entraîne une rotation double du genou, une rotation du genou entraîne une rotation du pied.
La cinématique inverse ou « inverse kinematics » (IK) :
Cette cinématique prend le problème dans l’autre sens : elle calcule les transformations à appliquer aux objets plus haut dans la hiérarchie pour obtenir une transformation sur un objet considéré.
Cette méthode est très efficace pour obtenir un mouvement réaliste de personnage : comme par exemple les mouvement du corps lorsqu’un personnage pose une main à terre. En « tirant » sur la main du personnage pour l’amener au sol, le bras se tend, le haut du corps se courbe et ensuite les hanches pivotent et se déplacent vers l’arrière (équilibre).

la technique de lien hiérarchique est utilisée pour les mouvements des planètes du système solaire dans le programme « Solar » expliqué en annexe.
La technique à base de script a pour principe de modéliser les mouvements comme on conçoit un programme informatique : « Le script est un programme principal dont le déroulement produit l’animation complète d’une scène » [Cou95].
Les scripts possèdent leur propre langage qui permet de définir les mouvements mais aussi les objets (souvent CSG).
Un acteur de l’animation peut être considéré comme un sous-script du script principal dont la but est le contrôle d’un objet particulier.
Mais les scripts peuvent également être une liste de fichiers (dans leur propre format) qui déterminent les positions, image par image, des éléments de la scène.
Cette technique d’animation est utilisée pour les positions des atomes dans le programme « MoleView » expliqué dans le chapitre suivant.
Dans l’animation contrôlée par la dynamique, les objets sont animés par des données physiques : gravité, forces, masse et contraintes éventuelles.
Par exemple : les mouvements de planètes avec les formules de gravitation universelle, les collisions d’objets ou encore les mouvements des molécules au niveau moléculaire.
Les mouvements générés dépendent de la véracité et la complétude des formules utilisées.
Dans le cas des collisions, il est essentiel de les détecter et de pouvoir réagir en conséquence : une technique simple est d’entourer les objets d’une enveloppe sphérique et de calculer la distance entre chaque objet afin de voir si ces objets sont en contact.
Cette méthode a le désavantage d’être gourmande en temps de calcul. On l’utilise en général pour générer des fichiers scripts qui peuvent être utilisés en différé.
C’est cette technique qui à été utilisée par les programmes du service de modélisation moléculaire pour générer les fichiers points utilisés dans le programme « Moleview » expliqué dans le chapitre suivant.
La librairie « GL_PLUS » expliquée dans le chapitre qui suit à été mise au point afin de pouvoir visualiser une simulation de substrat en temps réel.
La forme la plus simple de ce type d’animation est la modélisation de mouvements en fonction d’un modèle mathématique.
Par exemple une trajectoire de véhicule, une pièce de monnaie qui roule.
Mais cette technique, si elle est appliquée à des systèmes de particules peut, par exemple, modéliser de la fumée, des flammes ou des nuages.
Cette technique peut également générer des animations de vagues ou de torsions.
Cette technique consiste à modéliser le mouvement , les déformations, les changements de couleurs par une fonction mathématique : on crée par exemple une procédure qui génère les transformations appliquées aux objets en caoutchouc qui tombent (mouvement vertical vers le bas, écrasement et mouvement vertical vers le haut) ou une procédure qui dilate un gaz.
Cette technique d’animation est utilisée pour les mouvements de l’engin spatial dans le programme « Solar » expliqué en annexe.
La « motion capture » est une technique qui vise à enregistrer des mouvements réels de personnages.
Les techniques que nous avons vues jusqu’ici était des techniques artificielles d’imitation du mouvement mais ces techniques ne donnent en général que de pâles imitations dans le cas de mouvement animal ou humain.
La « motion capture » est un procédé qui consiste à enregistrer les mouvements d’un sujet humain ou animal , deux techniques existent :
Soit l’acteur est recouvert d’un « datasuit » et de « dataglove » (costume adapté) : les mouvement de l’acteur sont alors enregistrés par les capteur inclus dans le costume.
Soit en filmant de deux points de vue différents les mouvements d’un acteur .
Pour capter les mouvements de l’acteur, on lui colle des pastilles réfléchissantes sur les articulations. Par un travail de filtrage de l’image on élimine tout sauf les capteurs. Ce qui permet d’obtenir les mouvements relatifs des points d’articulations du corps humain.
Cette technique permet l'acquisition sur des relativement grandes surfaces (course de l’acteur, etc..) et libère de la contrainte des câbles reliant les capteurs au système informatique de la première méthode.
Jusqu’à présent, c’est cette technique qui donne le meilleur résultat pour les animations d’êtres humains.
Le terme « réalité virtuelle » est vague, il n’existe pas de définition précise de ce qu’est la réalité virtuelle.
Sous son aspect le plus médiatique, la réalité virtuelle est présentée comme une technologie révolutionnaire permettant de traverser l’écran de l’ordinateur pour accéder à un monde artificiel en trois dimensions.
Plus précisément, elle est présentée comme :
« La réalité virtuelle recouvre les concepts d'images de synthèse 3D, d'interactivité et surtout d'immersion dans le monde 3D. » par Neurone production.
« La réalité virtuelle est un monde artificiel avec ses composants propres et une nouvelle sorte d’expérience sensorielle de regarder, d’écouter de toucher, de manipuler des objets ou de parcourir des espace tous bien sûr virtuel » [Cou95].
Pour ma part je la définirais comme la représentation tridimensionnelle d'un espace réel ou fictif , tous les moyens qui accentuent l’immersion dans ce monde : ce sont les images, les sons et tous les moyens d’interactions avec le monde virtuel.
La réalité virtuelle se présente comme la suite logique à l’évolution de l’imagerie informatique. L’univers des images de synthèse, aussi réaliste soit-il, n’autorise pas l’homme à y pénétrer : celui-ci reste un spectateur inactif devant l’écran de sa station de travail. La réalité virtuelle permet d’entrer dans ce monde et d’interagir avec celui-ci. Cette nouvelle possibilité a ouvert de nouveaux horizons à l’imagerie sur ordinateur, que ce soit pour l’entraînement de pilotes, l’architecture, la conception assistée par ordinateur, l’ergonomie ou la recherche scientifique.
Dans cette partie de l’exposé, nous allons tout d’abord nous intéresser aux instruments matériels qui ont permis le passage d’un utilisateur passif à un utilisateur actif. Nous nous attarderons sur les périphériques spécifiques à la réalité virtuelle.
Nous nous intéresserons aux domaines professionnels où la réalité virtuelle est présente. Les domaines où la réalité virtuelle apporte un plus mais aussi ceux où elle s’avère être un partenaire intéressant et bon marché.
Ensuite nous nous attarderons sur l’apport de la réalité virtuelle dans le domaine de la recherche scientifique et plus particulièrement dans la simulation des phénomènes de mouillage et de la dynamique moléculaire en général.
Enfin nous terminerons ce chapitre par un bref aperçu du cas particulier de l’animation temps réel et au futur de la réalité virtuelle.
La réalité virtuelle est née de la réunion du son, de l’image de synthèse et des moyens d’interactions avec ces deux composants.
La qualité d’une application de réalité virtuelle se mesure par le taux d’immersion physique et mentale dans cette réalité fabriquée. L’immersion mentale est directement liée à l’immersion physique : l’immersion mentale est d’autant plus grande que l’immersion physique est grande.
Pour l’immersion physique, la réalité virtuelle utilise des périphériques spécifiques qui permettent d’interagir avec le monde virtuel ou donnent l’illusion d’images tridimensionnelles.
Dans cette partie, nous allons donner un aperçu des périphériques spécifiques à la réalité virtuelle.
Ces périphériques sont classés en deux parties :
Les périphériques qui fournissent des informations à l’ordinateur : les capteurs, les « Dataglove » et « Datasuit », etc..
Les périphériques qui fournissent des informations à l’utilisateur : les « HMD », les lunettes stéréoscopiques, les générateurs de sons tridimensionnels, certains « Dataglove », etc...
Les capteurs :
Ce type de capteur a comme objectif de poursuivre les mouvement du corps de l’individu et particulièrement ceux de la tête et des mains .
Ce type de capteur est composé de trois parties un ou deux récepteurs au sol, d’émetteurs ( placés sur la tête, le dos et les mains) et d’une unité de contrôle qui détermine la position de l’émetteur par rapport aux récepteurs.
Il existe des capteurs magnétiques, à ultrason, à infra-rouges, etc...
Les capteurs de dernières générations déterminent le mouvements des personnes sans qu’ils n’aient plus d’émetteur, ils utilisent la même technique que le « motion capture » c’est-à-dire des surfaces réfléchissantes et deux caméras.
Les « Dataglove » et « Datasuit »:
Les gants de données également appelés « Dataglove » sont des gants équipés d’une multitude de capteurs qui fournissent en permanence à l’ordinateur des informations sur la position et l’orientation de la mains et des doigts. Ils permettent à l’utilisateur de saisir et de manipuler des objets avec sa propre main. Les capteurs de ces gants (mais aussi des « Datasuit ») sont des fibres de optiques qui se plient en même temps que les doigts : la diminution de l’intensité des rayons lumineux permet de calculer la courbure à la sortie des fibres.
Une évolution de ces gants a donné naissance aux retours tactiles qui permettent de donner l’illusion du toucher : ce sont des gants qui exercent une résistance variable par des systèmes tels que gonflement de ballons gonflables à l’intérieur du gants ou par un système de squelette exogène muni de pistons hydrauliques.
Par extension des « Dataglove », les « Datasuit » sont des combinaisons recouvrant le corps qui ont les mêmes composants et fonctions que les « Dataglove ».
Les lunettes stéréoscopiques
Ces lunettes stéréoscopiques sont des lunettes à cristaux liquides qui laissent alternativement l’œil droit et l’œil gauche voir une image.
L’ordinateur doit bien évidement afficher les images stéréoscopiques à une fréquence double (60 Hz) de celle de l’animation sans ces lunettes. De plus les images doivent être calculées en fonction de l’œil qui est capable de voir. De plus l’affichage doit être synchronisé avec l’ouverture des lunettes.
Le dispositif de commande de ces lunettes stéréoscopiques est incorporé en standard dans les stations de travail Silicon Graphics.
Ces lunettes incorporent des capteurs qui déterminent la position des yeux par rapport à l’écran (où sont placés des détecteurs), ce dispositif permet de changer l’angle de vue des images en réaction aux mouvement de tête.
Les » HMD » :

Les « HMD » ou Head Mounted Display sont des doubles écrans vidéos montés sur des lunettes (un point de vue de la scène par écran ).
En général, un capteur de position de la tête y est incorporé, permettant aux programmes de réalité virtuelle de calculer un point de vue correspondant à celui de l'utilisateur.
Les afficheurs à tube cathodique monochrome sont recouverts d'un filtre à cristaux liquides laissant voir un tiers du temps le tube sous filtre rouge, un tiers sous filtre bleu et un tiers sous filtre vert. Si le taux de rafraîchissement du tube est suffisamment rapide (en général 180 Hz), l’œil perçoit une image en couleurs animée à 60 images/seconde.
Il existe aussi des afficheurs couleurs à cristaux liquides. Les tailles se sont réduites à 2cm de diagonale environ, contribuant ainsi à la réduction de poids de l'ensemble.
Un exemple : les lunettes couleurs de RPI advanced Technology Group, nommées HMSI (Head Mounted Sensory Interface) pèsent moins de 200 grammes et ne font que trois centimètres d'épaisseur. De plus, il suffit d'enlever une pièce pour pouvoir les utiliser en mode semi-transparent pour superposer l'image de synthèse et la vision réelle.
les générateurs de sons tridimensionnels :
Les générateurs de sons tridimensionnels sont assez rares, c’est un casque stéréo classique muni de capteurs afin de connaître l’orientation et la position de la tête. L’orientation et la position de la tête définissent le volume des différents sons dans les écouteurs gauche et droit en fonction des réflexions des sons sur les objets de la scène.

Cette technique permet de mettre en concordance les sons et les images : elle a pour effet d’augmenter l’immersion mentale.
La réalité virtuelle, au fil des années s’est introduite dans le monde professionnel et le nombre d’applications s'accroît constamment.
Les systèmes sont maintenant tout à fait utilisables, même par des utilisateurs non programmeurs. Cette extension est due aux applications propres à chaque domaine qui permettent de créer un environnement virtuel en quelques minutes.
Les domaines d'applications actuels vont du design architectural et mécanique au simulateur de vol en passant par les jeux, la promotion de produits et la biochimie.
Par exemple, on peut observer un bâtiment sous tous ses angles. Il peut s'agir de l'espace des données dans un programme de calcul de structure où l'on visualise les tensions dans une pièce ou encore d'un monde imaginaire où évoluent des personnages de fiction, des tyrannosaures ou des jouets.
Dans l’industrie :
Les usages industriels de la réalité virtuelle sont innombrables. Ils ont commencé là où les produits manufacturés étaient les plus chers, comme dans la technique spatiale ou l'automobile, puis se sont vulgarisés. Il est devenu tout à fait courant d'utiliser un ordinateur pour visualiser un prototype d'œuf de Pâques en plastique aussi bien qu'une semelle de chaussure.
L’aspect le plus important est le prototypage rapide du produit :
Réduire le temps de fabrication d'un prototype passe par le prototypage rapide. Il ne s’effectue plus par des maquettes traditionnelles en bois ou plâtre. Les produits font l’objet d’une modélisation 3D et sont suivis directement par une phase de pilotage d'un périphérique réalisant directement la pièce.
Il existe plusieurs techniques pour passer directement de l'ordinateur au produit fini de prix et de qualité fort différents.
Il existe, par exemple, le « portique - fraiseuse à 3 axes » .
Cette technique est la plus utilisée, une fraiseuse à commande numérique est directement connectée, comme un périphérique, à l'ordinateur de CAO. Ce dernier peut, à tout moment, demander une copie sur la fraiseuse du modèle 3D qu'il a en mémoire. Un bloc de matière est directement usiné. Cette méthode est utilisée dans l'industrie automobile pour obtenir des modèles réduits au 1/10ème ou en grandeur nature à partir de blocs de matière plastique, usuellement du polystyrène. L'avantage de gain de temps par rapport aux méthodes manuelles est tout à fait considérable.
La « stéréolithographie » :
Un nouveau type de périphérique informatique a vu le jour ces dernières années, à l'initiative de la société « 3D systems »: les machines de coulée 3D. Il permet de réaliser un modèle d'une turbine complète avec tous ses aubages, son axe creux, etc. en une seule passe.
Une fois le modèle 3D réalisé, on y ajoute des supports pour la réalisation de la maquette. Un logiciel spécialisé découpe ensuite le modèle 3D en tranches 2D (de 65 à 700 microns d'épaisseur) et produit la succession de vecteurs que le laser devra parcourir.
Ensuite vient la phase de fabrication proprement dite : une cuve est pleine d'une résine epoxy très fluide qui polymérise en présence d'un rayonnement ultra-violet. Un plateau mobile est situé juste sous la surface du liquide. Il peut descendre doucement durant le processus. Un laser à rayonnement ultra-violet dessine sur la surface du liquide un balayage qui correspond à la «tranche» inférieure de l'objet. La résine située entre le plateau et la surface durcit (sur une épaisseur d'une fraction de millimètre). Ensuite, le plateau descend légèrement et le processus recommence pour la tranche suivante de l'objet à modéliser. L'épaisseur d'une tranche varie de 0.125 mm à 0.75 mm. L'objet est ainsi construit par tranches horizontales successives. Après retrait du liquide, la pièce est débarrassée de ses supports et nettoyée. Elle termine son durcissement dans un four à rayonnement UV.
Cette technique ne permet pas de réaliser des pièces fonctionnelles, mais elle donne rapidement des modèles d'objets de forme très complexes.
Les simulations :
Les simulations occupent également une place importante dans les domaines professionnels, que ce soit pour des simulateurs de conduite, de résultats, de déformations de matière ou de déroulement d’actions.
Leur intérêt principal réside dans leur faible coût en regard de ce qui est simulé .
Les simulateurs de vol ou de conduite de train ne coûtent plus qu'une faible fraction de l'appareil qu'ils simulent et sont devenus irremplaçables.
La construction d’une maquette de maison permet à l’architecte de montrer à son client sa future maison dans laquelle on peut se balader «en temps réel» sur un simple PC . La simulation est ici d’un acteur de promotion du produit beaucoup moins cher qu’une maquette de bois.
Les ergonomistes utilisent déjà « Jack », un mannequin de synthèse, pour tester la maniabilité des créations des designers avant leur réalisation. Ce mannequin permet de simuler les mouvements d’un pilote afin de tester l’ergonomie d’un cockpit sans avoir à le créer.
Chez VOLVO, un simulateur d’accident permet de tester les déformations d’une voiture. Ce type de simulation permet d’économiser une voiture à chaque test. De plus, la déformation peut être observée sous tous les angles et peut être isolée pièce par pièce.
Quant à l'industrie du cinéma, elle crée en 3D des prototypes bon marché de décors avant même d'écrire un scénario et des décors plus précis pour le film. Après avoir mesuré les déplacement de la caméra en présence des acteurs sur fond bleu, les mouvements de la caméra réelle sont alors simulés dans le décor virtuel. L’apport de ces modélisations de décor diminue considérablement le coût des films.

La technique inverse à été utilisée pour le projet « RACOON » de la régie Renault : un prototype de voiture à été superposé à un décors réel en vue de voir si le design du prototype pouvait s’inscrire dans la vie de tous les jours.
Nous pouvons également parler des simulateurs de largage en apesanteur de satellites ou d’arrimage de navettes à une station spatiale qui sont techniquement impossibles en dehors de la simulation.
Dans les jeux vidéo :
Une part non négligeable des consommateurs d’images de synthèse est l’industrie des jeux vidéo : Nintendo, Sega et Sony, les trois plus gros vendeurs de jeux électroniques, utilisent cinq fois plus d'heures d'images animées que toutes les autres professions réunies [L&M94].
Afin d’accroître l’intérêt pour leur jeux ces sociétés truffent leurs jeux d’images de synthèse. Les jeux 3D occupent le devant de la scène des ventes au point que le chiffre d'affaires de ce secteur aux USA est supérieur à celui du cinéma.
Que ce soit pour les simulateurs, les jeux de stratégie ou les jeux de combat, les jeux vidéo regorgent de 3D. Les consoles actuelles sont entièrement dédiées à la 3D, elles sont dotées de processeurs graphiques et d’unités centrales conçus pour la 3D comme les processeurs 3DFx des cartes graphiques ou les processeurs de Silicon Graphics pour les unités centrales.
Archéologie :
Une réalisation récente d’une société française a permis de reconstituer le Panthéon à partir des ruines : cette réalisation a permis entre autre de visualiser pour la première fois le Panthéon dans sa forme originelle. Les archéologues on pu en déduire le niveau de connaissance réelle des grecques en architecture.
Nous pouvons également citer la reconstitution de l’abbaye de Cluny qu’il est possible de visiter virtuellement. Cette visite à été réalisée en première mondiale dans la salle de Forum Imagina 93 à l’initiative de l’INA (Institut National de l’Audiovisuel en France).
Mais la réalité s’applique également à la reconstitution de squelettes d’espèces disparues en vue d’analyser les mouvements de ces espèces et de reconstituer leur aspect en fonction de leur squelette.
Dans le domaine de la recherche :
Le fait de pouvoir visualiser l'inaccessible apporte beaucoup dans le domaine de la recherche .
En médecine, les étudiants peuvent trouver sur Internet ou sur CD-ROM une maquette en trois dimensions du corps humain. Cette maquette à été réalisée en découpant un véritable être humain en fines tranches. Cette modélisation permet de décomposer le corps humain, d’isoler certaines parties, suivre les vaisseaux, etc.

Mais le domaine de recherche où les images de synthèse sont le plus présentes est la modélisation moléculaire : le fait de pouvoir filmer sans les contraintes physiques d’une véritable caméra permet de modéliser les atomes et de pouvoir voir au niveau moléculaire le comportement de la matière. La visualisation en 3D des molécules est devenue un des outils de base des physiciens, chimistes biochimistes et des généticiens.

La réalité virtuelle est une discipline nouvelle qui, aidée par les progrès techniques considérables, n’a pas encore livré toutes ses possibilités.
La simulation d’évacuation du « Stade de France » peuplé de supporters virtuels laisse entrevoir les possibilités en terme de sécurité que peut apporter la réalité virtuelle.
Les systèmes de commandes temps réel de marionnette virtuelle, tel que le système PORC utilisé dans l’émission « CiberFlash » de Canal+, ouvre la porte à un nouveau genre de présentateur de télévision.

Animation en temps réel : système PORC ( © Médialab, Paris)
Dans le domaine du jeu ou du film interactif, les travaux de N. et D.Thalmann ouvrent la voie à la réalisation de vrais acteurs synthétiques, ayant leur propre comportement individuel et doués d'une intelligence, voire d'une personnalité propre.

Certains médecins ont déjà testé un dispositif de réalité virtuelle permettant de superposer, grâce à des lunettes spéciales, une radiographie 3D et la vision réelle du patient qu'ils sont en train d'opérer (projet PACE).
Le développement d’outils propre à la télécommunication via Internet tel que VRML permet d’entrevoir des forums de discussions dans des lieux totalement crées ou reconstitués. Des visites guidées de lieux détruits ou inaccessibles.
Pourquoi ne pas imaginer des vacances dans un jardin d’Eden virtuel ou une galerie d’art virtuel.
La seule limite à la réalité virtuelle est l’imagination.